模型选择与评估

损失函数类

代价函数，损失函数和目标函数的区别？

损失函数（Loss Function ）是定义在单个样本上的，算的是一个样本的误差。
代价函数（Cost Function）是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均。
目标函数（Object Function）定义为：最终需要优化的函数。等于经验风险+结构风险（也就是代价函数 + 正则化项）。代价函数最小化，降低经验风险，正则化项最小化降低。
风险函数(risk function)，风险函数是损失函数的期望，这是由于我们输入输出的(X,Y)遵循一个联合分布，但是这个联合分布是未知的，所以无法计算。但是我们是有历史数据的，就是我们的训练集，f(x) 关于训练集的平均损失称作经验风险(empirical risk)，即，所以我们的目标就是最小化称为经验风险最小化。

误差、偏差和方差的区别是啥？

噪声：描述了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。说人话，就是数据中的有些标签不是真的标签，也是有限噪声的标签。

偏差：是指预测结果与真实值之间的差异，排除噪声的影响，偏差更多的是针对某个模型输出的样本误差，偏差是模型无法准确表达数据关系导致，比如模型过于简单，非线性的数据关系采用线性模型建模，偏差较大的模型是错的模型。

方差：不是针对某一个模型输出样本进行判定，而是指多个(次)模型输出的结果之间的离散差异，注意这里写的是多个模型或者多次模型，即不同模型或同一模型不同时间的输出结果方差较大，方差是由训练集的数据不够导致，一方面量 (数据量) 不够，有限的数据集过度训练导致模型复杂，另一方面质(样本质量)不行，测试集中的数据分布未在训练集中，导致每次抽样训练模型时，每次模型参数不同，输出的结果都无法准确的预测出正确结果。

常见的损失函数有哪些？

0-1损失函数
0-1损失是指，预测值和目标值不相等为1，否则为0
绝对值损失函数平方损失函数（squared loss）
实际结果和观测结果之间差距的平方和，一般用在线性回归中，可以理解为最小二乘法
对数损失函数（logarithmic loss）这个在逻辑回归中用到的
指数损失函数，这个在Adaboost中就有体现的
铰链损失函数，这个在SVM中用到过

均方差损失函数和高斯假设的关系？

事先我们模型预测与真实值之间的误差是服从标准高斯分布也就是$\mu {\rm{ = }}0,\sigma {\rm{ = }}1$，我们给定一个输入$x_i$，则模型输出真实值$y_i$的概率为:

$$ p({y_i}|{x_i}) = \frac{1}{{\sqrt {2\pi } }}\exp ( - \frac{{{{({y_i} - {{\hat y}_i})}^2}}}{2}) $$

再假设各个样本点之间是相互独立的，那么最大似然函数可以写为：

$$ L(x,y) = \prod\limits_{i = 1}^N {\frac{1}{{\sqrt {2\pi } }}} \exp ( - \frac{{{{({y_i} - {{\hat y}_i})}^2}}}{2}) $$

为了计算方便，通常取对数似然函数，结果如下：

$$ \log L(x,y) = - \frac{N}{2}\log 2\pi - \frac{1}{2}\sum\limits_{i = 1}^N {{{({y_i} - {{\hat y}_i})}^2}} $$

可以看到前面的一项是C，只与后面的结果有关，然后转化为最小化负对数似然 Negative Log-Likelihood

$$ - \log L(x,y) = \frac{1}{2}\sum\limits_{i = 1}^N {{{({y_i} - {{\hat y}_i})}^2}} $$

这就是MSE的基本形式，也就是说在假设误差为高斯分布的情况下，最小化均方差损失函数与极大似然估计本质上是一致的。

平均绝对误差损失函数和拉普拉斯假设的关系？

事先我们模型预测与真实值之间的误差是服从拉普拉斯分布也就是$\mu {\rm{ = }}0,b {\rm{ = }}1$，我们给定一个输入$x_i$，则模型输出真实值$y_i$的概率为:

$$ p({y_i}|{x_i}) = \frac{1}{2}\exp ( - |{y_i} - {{\hat y}_i}|) $$

和上面的推导类似，最后可以得到如下的公式：

$$ - \log L(x,y) = \frac{1}{2}\sum\limits_{i = 1}^N {(|{y_i} - {{\hat y}_i}|)} $$

这就是MAE我的基本形式，也就是说在假设误差为拉普拉斯分布的情况下，最小化均方差损失函数与极大似然估计本质上是一致的。

均方差损失函数与平均绝对误差损失函数区别?

通过上述分析我们可以发现，MSE损失相对于MAE会更加快速的收敛，但是MAE相比于异常点会更健壮。

当使用梯度下降算法时，MSE 损失的梯度为$-{ \hat y }$，而 MAE 损失的梯度为$\pm 1$，即 MSE 的梯度的值会随误差大小而变化，而 MAE 的梯度的则一直保持为 1，即便在绝对误差$|{y_i} - {\hat y_i}|$很小的时候 MAE 的梯度也同样保持为 1，这实际上是非常不利于模型的训练的，也就是我们看到的训练的时候呈现上下左右直线跳的现象。

从上述的损失函数计算公式中我们也可以看到，MSE的公式中有平方项，这样当数据中存在较大的异常值的话会导致较大的异常的梯度，但MAE就不会，梯度就是1，就是这么拽。

mse对于异常样本的鲁棒性差的问题怎么解决？

如果异常样本无意义，可以进行异常值的平滑或者直接删除。
如果异常样本有意义，需要模型把这些有意义的异常考虑进来，则从模型侧考虑使用表达能力更强的模型或复合模型或分群建模等；
在损失层面选择更鲁棒的损失函数例如smape

介绍你了解到的熵的相关知识点？

信息量
度量一个事件的不确定性程度，不确定性越高则信息量越大，一般通过事件发生的概率来定义不确定性，信息量则是基于概率密度函数的log运算，用以下式子定义：

$$ I(x) = - \log p(x) $$

信息熵
衡量的是一个事件集合的不确定性程度，就是事件集合中所有事件的不确定性的期望，公式定义如下：

$$ H(X) = - \sum\limits_{x \in X} {[p(x)\log p(x)]} $$

相对熵(KL散度)
kl散度，从概统角度出发，表示用于两个概率分布的差异的非对称衡量，kl散度也可以从信息理论的角度出发，从这个角度出发的kl散度我们也可以称之为相对熵，实际上描述的是两个概率分布的信息熵的差值：

$$ KL(P||Q) = \sum {P(x)\log \frac{{P(x)}}{{Q(x)}}} $$

kl散度和余弦距离一样，不满足距离的严格定义；非负且不对称。

js散度
公式如下：

$$ JS(P||Q) = \frac{1}{2}KL(P(x))||\frac{{P(x) + Q(x)}}{2} + \frac{1}{2}KL(Q(x))||\frac{{P(x) + Q(x)}}{2} $$

js散度的范围是[0,1],相同则是0，相反为1。相较于KL，对相似度的判别更准确;同时，js散度满足对称性 JS(P||Q)=JS(Q||P)

交叉熵
公式如下：

$$ H(P,Q) = - \sum {p\log q = H(P) + {D_{kl}}(P||Q)} $$

可见,交叉熵就是真值分布的信息熵与KL散度的和,而真值的熵是确定的,与模型的参数θ 无关,所以梯度下降求导时，优化交叉熵和优化kl散度（相对熵）是一样的；

联合熵
公式如下：

$$ H(X,Y) = - \sum\limits_{x,y} {p(x,y)\log p(x,y)} $$

联合熵实际上衡量的是两个事件集合，经过组合之后形成的新的大的事件集合的信息熵；

条件熵
公式如下：

$$ H(Y|X) = H(X,Y) - H(X) $$

事件集合Y的条件熵=联合熵-事件集合X的信息熵，用来衡量在事件集合X已知的基础上，事件集合Y的不确定性的减少程度；

交叉熵的设计思想是什么？

优化交叉熵等价于优化kl散度

$$ H(P,Q) = - \sum {p\log q = H(P) + {D_{kl}}(P||Q)} $$

这里的P是真实分布，它的信息熵 H（p）是一个定值，对于模型来说是一个不可优化的常数, 因此优化的时候可以忽略。

怎么衡量两个分布的差异？

使用KL散度或者JS散度

Huber Loss 有什么特点？

首先看下huber loss的形状：

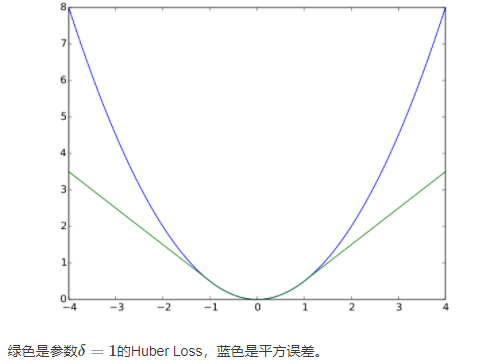
Huber Loss 结合了 MSE 和 MAE 损失，在误差接近 0 时使用 MSE，使损失函数可导并且梯度更加稳定；在误差较大时使用 MAE 可以降低 outlier 的影响，使训练对 outlier 更加健壮。缺点是需要额外地设置一个超参数。

为何使用Huber损失函数？

使用MAE用于训练神经网络的一个大问题就是，它的梯度始终很大，这会导致使用梯度下降训练模型时，在结束时遗漏最小值。对于MSE，梯度会随着损失值接近其最小值逐渐减少，从而使其更准确。
在这些情况下，Huber损失函数真的会非常有帮助，因为它围绕的最小值会减小梯度。而且相比MSE，它对异常值更具鲁棒性。因此，它同时具备MSE和MAE这两种损失函数的优点。不过，Huber损失函数也存在一个问题，我们可能需要训练超参数δ，而且这个过程需要不断迭代。

如何理解Hinger Loss？

首先看下Hinger Loss的图像，如下：

可以看到，当x大于某个值的时候，loss为0，当x小于某个值的时候，那就需要算loss了，说明模型对小于阈值的样本进行了惩罚，而且越大惩罚的越厉害，对于大于阈值的样本不进行惩罚，总的来说就是该损失函数寻找一个边界，对具有可信的样本不惩罚，对不可信的样本或者超出决策边界的样本进行惩罚。

交叉熵与最大似然估计的联系？

交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近，即拟合的更好。
最小化交叉熵即最小化KL散度，即最小化实际与预估之间的差距，这与最大似然的目的是一致的。即最大似然与交叉熵在目标上一致，只是由于正负号，而导致一个为最小化（交叉熵，前面有负号），一个为最大化（最大似然）

分类问题为何用交叉熵而不用MSE？

首先来看两者的表达式
MSE的表达式如下：

$$ L = \frac{1}{N}\sum\limits_{i = 1}^N {||{y_i} - {{\hat y}_i}|{|^2}} $$

交叉熵的表达式如下：

$$ L = \frac{1}{N}\sum\limits_{i = 1}^N {\sum\limits_{k = 1}^N {{y_i}^k\log {{\hat y}_i}^k} } $$

可以看到，对于分类问题，实际的标签为0和1，那么交叉熵很多项是不用算的，举个例子，实际标签是[1,0,0],模型预测得到的概率是[0.9,0.4,0.3],那么交叉熵损失函数的结果是 1log(0.9)+0log(0.4)+0log(0.3),而MSE则都得全部算一遍。
结论1：MSE无差别得关注全部类别上预测概率和真实概率的差.交叉熵关注的是正确类别的预测概率。
其次，我们在之前的文章中也说到了关于求解优化模型的时候的问题，MSE会收敛的慢一些，因为它求导的结果相比于交叉熵还多乘以一个sigmod函数，但是交叉熵梯度中不再含有sigmoid的导数，有的是sigmoid的值和实际值之间的差，也就满足了我们之前所说的错误越大，下降的越快的要求。
结论2：是交叉熵更有利于梯度更新。
MSE是假设数据符合高斯分布时,模型概率分布的负条件对数似然;交叉熵是假设模型分布为多项式分布时,模型分布的负条件对数似然。
还有一点要说明，MSE对残差大的样例惩罚更大些.，我们还举个例子看看，比如真实标签分别是(1, 0, 0).模型1的预测标签是(0.8, 0.2, 0),模型2的是(0.9, 0.1, 0). 但MSE-based算出来模型1的误差是MSE-based算出模型2的4倍,而交叉熵-based算出来模型1的误差是交叉熵-based算出来模型2的2倍左右.对于模型1和模型2输出的结果。其实也主要是由于MSE太苛刻了，想要把左右的值都预测的分毫不差，而交叉熵只关注正样本也也是就1的那些，计算那些损失函数就可以了，样本标签为0的压根不用算。

类别不均衡情况下使用什么损失函数？

可以使用Focal loss函数：为了解决正负样本严重失衡的问题，由 log loss 改进而来

$$ {L_{FL}} = - \frac{1}{n}\sum\limits_{i = 1}^N {[\alpha {y_i}{{(1 - {{\hat y}_i})}^\gamma }\log {{\hat y}_i} + (1 - \alpha )(1 - {y_i}){{\hat y}_i}^\gamma \log (1 - {{\hat y}_i})]} $$

基本思想：对于类别极度不平衡的情况下，网络如果在 log loss 下会倾向于之预测负样本，并且负样本的预测概率$ {{{\hat y}_i}} $ 也会非常的高，回传的梯度也很大。但是如果添加${(1 - {\hat y_i})^\gamma }$则会使预测概率大的样本得到的 loss 变小，而预测概率小的样本，loss 变得大，从而加强对正样本的关注度。可以改善目标不均衡的现象，对此情况比交叉熵要好很多。

参考

https://zhuanlan.zhihu.com/p/358103958
https://zhuanlan.zhihu.com/p/149093389
https://zhuanlan.zhihu.com/p/376387915
https://zhuanlan.zhihu.com/p/77686118
https://blog.csdn.net/Scc_hy/article/details/84190080
https://zhuanlan.zhihu.com/p/391954665
https://www.zhihu.com/collection/168981231

偏差与方差

什么是偏差和方差？

不要看这个问题简单，但是问的时候，真的一下子你可能会答不上来。偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力;方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。

什么是噪声？

噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。噪声的存在是学习算法所无法解决的问题，数据的质量决定了学习的上限。假设在数据已经给定的情况下，此时上限已定，我们要做的就是尽可能的接近这个上限。举个简单的例子，对于一个预测性别的任务来说，特征中有胡子，标签为女性，这样的数据就是噪声数据，它反应的是数据质量的问题。

泛化误差、偏差和方差的关系？

关系如下：
$E = bia{s^2}(x) + {\mathop{\rm var}} (x) + {\varepsilon ^2}$
也就是说，泛化误差可以通过一系列公式分解运算证明：泛化误差为偏差、方差与噪声之和。证明过程如下：

“偏差-方差分解”说明，泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。

偏差、方差与过拟合、欠拟合的关系？

一般来说，简单的模型会有一个较大的偏差和较小的方差，复杂的模型偏差较小方差较大。

欠拟合：模型不能适配训练样本，有一个很大的偏差。

举个例子：我们可能有本质上是多项式的连续非线性数据，但模型只能表示线性关系。在此情况下，我们向模型提供多少数据不重要，因为模型根本无法表示数据的基本关系，模型不能适配训练样本，有一个很大的偏差，因此我们需要更复杂的模型。那么，是不是模型越复杂拟合程度越高越好呢？也不是，因为还有方差。

过拟合：模型很好的适配训练样本，但在测试集上表现很糟，有一个很大的方差。

方差就是指模型过于拟合训练数据，以至于没办法把模型的结果泛化。而泛化正是机器学习要解决的问题，如果一个模型只能对一组特定的数据有效，换了数据就无效，我们就说这个模型过拟合。这就是模型很好的适配训练样本，但在测试集上表现很糟，有一个很大的方差。

偏差、方差与模型复杂度的关系?

复杂度高的模型通常对训练数据有很好的拟合能力，但是对测试数据就不一定了。而复杂度太低的模型又不能很好的拟合训练数据，更不能很好的拟合测试数据。因此，模型复杂度和模型偏差和方差具有如下图所示关系

请从偏差和方差的角度解释bagging和boosting的原理？

偏差指的是算法的期望预测与真实值之间的偏差程度，反映了模型本身的拟合能力；方差度量了同等大小的训练集的变动导致学习性能的变化，刻画了数据扰动所导致的影响。

Bagging对样本重采样，对每一重采样得到的子样本集训练一个模型，最后取平均。由于子样本集的相似性以及使用的是同种模型，因此各模型有近似相等的bias和variance。由于$E[\frac{{\sum {{X_i}} }}{n}] = E[{X_i}]$，所以bagging后的bias和单个子模型的接近，一般来说不能显著降低bias。另一方面，若各子模型独立，则有$Var[\frac{{\sum {{X_i}} }}{n}] = \frac{{Var[{X_i}]}}{n}$，此时可以显著降低variance。若各子模型完全相同，则$Var[\frac{{\sum {{X_i}} }}{n}] = Var[{X_i}]$，此时不会降低variance。

bagging方法得到的各子模型是有一定相关性的，属于上面两个极端状况的中间态，因此可以一定程度降低variance。

boosting从优化角度来看，是用forward-stagewise这种贪心法去最小化损失函数,由于采取的是串行优化的策略，各子模型之间是强相关的，于是子模型之和并不能显著降低variance。所以说boosting主要还是靠降低bias来提升预测精度。

为什么说bagging是减少variance，而boosting是减少bias?

boosting是把许多弱的分类器组合成一个强的分类器。弱的分类器bias高，而强的分类器bias低，所以说boosting起到了降低bias的作用。variance不是boosting的主要考虑因素。bagging是对许多强（甚至过强）的分类器求平均。在这里，每个单独的分类器的bias都是低的，平均之后bias依然低；而每个单独的分类器都强到可能产生overfitting的程度，也就是variance高，求平均的操作起到的作用就是降低这个variance。

如何解决偏差、方差问题？

偏差和方差是无法完全避免的，只能尽量减少其影响。
(1) 在避免偏差时，需尽量选择正确的模型，一个非线性问题而我们一直用线性模型去解决，那无论如何，高偏差是无法避免的。
(2) 有了正确的模型，我们还要慎重选择数据集的大小，通常数据集越大越好，但大到数据集已经对整体所有数据有了一定的代表性后，再多的数据已经不能提升模型了，反而会带来计算量的增加。而训练数据太小一定是不好的，这会带来过拟合，模型复杂度太高，方差很大，不同数据集训练出来的模型变化非常大。
(3) 最后，要选择合适的模型复杂度，复杂度高的模型通常对训练数据有很好的拟合能力。

训练集上预测误差大，在测试集上预测误差小的情况？

模型恰好在验证数据上的泛化性能好，例如二分类问题中，测试集数据恰好是和分界超平面距离很远的样本或者是回归问题中，验证数据在模型的拟合曲面上。

参考

https://zhuanlan.zhihu.com/p/38853908
https://www.zhihu.com/question/27068705
https://www.zhihu.com/question/27068705/answer/416457469
https://www.zhihu.com/collection/168981231

过拟合和欠拟合

什么是欠拟合？

欠拟合是指模型不能在训练集上获得足够低的误差。换句换说，就是模型复杂度低，模型在训练集上就表现很差，没法学习到数据背后的规律。

什么是过拟合？

过拟合是指训练误差和测试误差之间的差距太大。换句换说，就是模型复杂度高于实际问题，模型在训练集上表现很好，但在测试集上却表现很差。模型对训练集"死记硬背"（记住了不适用于测试集的训练集性质或特点），没有理解数据背后的规律，泛化能力差。

如何解决欠拟合?

添加其他特征项。组合、泛化、相关性、上下文特征、平台特征等特征是特征添加的重要手段，有时候特征项不够会导致模型欠拟合。
添加多项式特征。例如将线性模型添加二次项或三次项使模型泛化能力更强。例如，FM（Factorization Machine）模型、FFM（Field-aware Factorization Machine）模型，其实就是线性模型，增加了二阶多项式，保证了模型一定的拟合程度。
可以增加模型的复杂程度。
减小正则化系数。正则化的目的是用来防止过拟合的，但是现在模型出现了欠拟合，则需要减少正则化参数。

过拟合原因有哪些？

（1）建模样本选取有误，样本标签错误等，导致选取的样本数据不足以代表预定的分类规则
（2）样本噪音干扰过大，使得机器将学习了噪音，还认为是特征，从而扰乱了预设的分类规则
（3）假设的模型无法合理存在，或者说是假设成立的条件实际并不成立
（4）参数太多，模型复杂度过高
（5）对于tree-based模型，如果我们对于其深度与split没有合理的限制，有可能使节点只包含单纯的事件数据(event)或非事件数据(no event)，使其虽然可以完美匹配（拟合）训练数据，但是无法适应其他数据集
（6）对于神经网络模型：1.权值学习迭代次数太多(Overtraining)，2。BP算法使权值可能收敛过于复杂的决策面

如何解决过拟合?

重新清洗数据，数据不纯会导致过拟合，此类情况需要重新清洗数据。
增加训练样本数量。
降低模型复杂程度。
增大正则项系数。
采用dropout方法。
early stopping。
减少迭代次数。
增大学习率。
添加噪声数据。
树结构中，可以对树进行剪枝。
减少特征项。

欠拟合和过拟合这些方法，需要根据实际问题，实际模型，进行选择。

为什么L1正则化会产生更稀疏？

L1中的参数更新如下所示：

$$ w \to w' = w - \frac{{\eta \lambda }}{n}{\mathop{\rm sgn}} (w) - \eta \frac{{\partial {C_0}}}{{\partial w}} $$

其中$C_0$是损失函数，$n$是样本数，$\lambda$是正则参数，我们看这个参数更新的公式，发现

$w=0$, 时，$w=0$是不可导的。所以我们仅仅能依照原始的未经正则化的方法去更新$w=0$。
当 $w>0$ 时，$sgn(w)>0$, 则梯度下降时更新后的$w$变小。
当 $w<0$ 时，$sgn(w)<0$, 则梯度下降时更新后的$w$变大，换句换说，L1正则化使得权重$w$往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。

为啥L1正则先验分布是Laplace分布，L2正则先验分布是Gaussian分布

L1正则先验分布是Laplace分布，L2正则先验分布是Gaussian分布。接下来从最大后验概率的角度进行推导和分析。在机器学习建模中，我们知道了$x$和$y$以后,需要对参数$w$进行建模。那么后验概率表达式如下:

$$ MAP = \log P(y|X,w)P(w) = \log P(y|X,w) + \log P(w) $$

可以看出来后验概率函数为在似然函数的基础上增加了$logP(w)$，$P(w)$的意义是对权重系数$w$的概率分布的先验假设，在收集到训练样本$X$，$y$
后，则可根据$w$在$X$，$y$
下的后验概率对$w$进行修正，从而做出对的更好地估计。若假设$w$的先验分布为0均值的高斯分布，即 $w \sim N(0,{\sigma ^2})$,则有

$$ \log P(w) = \log \prod\limits_j {P({w_j}) = } \log \prod\limits_j {[\frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{w_j}^2}}{{2{\sigma ^2}}}}}] = - \frac{1}{{2{\sigma ^2}}}} \sum\limits_j {{w_j}^2 + C} $$

可以看到，在高斯分布$logP(w)$下的效果等价于在代价函数中增加L2正则项。若假设服$w$从均值为0，参数为a的拉普拉斯分布，即$P({w_j}) = \frac{1}{{\sqrt {2a} }}{e^{\frac{{|{w_j}|}}{a}}}$，则有

$$ \log P(w) = \log \prod\limits_j {P({w_j}) = } \log \prod\limits_j {\frac{1}{{\sqrt {2a} }}{e^{\frac{{|{w_j}|}}{a}}}} = - \frac{1}{{2a}}\sum\limits_j {|{w_j}| + C} $$

可以看到，在拉普拉斯分布$logP(W)$下的效果等价在代价函数中增加L1正项。

L1正则化可通过假设权重w的先验分布为拉普拉斯分布，由最大后验概率估计导出。

L2正则化可通过假设权重w的先验分布为高斯分布，由最大后验概率估计导出。

Lasso回归的求解方法有哪些？

Lasso回归有时也叫做线性回归的L1正则化，和Ridge回归的主要区别就是在正则化项，Ridge回归用的是L2正则化，而Lasso回归用的是L1正则化。由于L1范数用的是绝对值之和，在零点处不可求导，所以使用非梯度下降法进行求解，如坐标轴下降法（coordinate descent）和最小角回归法（ Least Angle Regression， LARS）。

坐标轴下降法
坐标轴下降法坐标下降优化方法是一种非梯度优化算法，坐标下降算法每次选择一个维度进行参数更新，维度的选择可以是随机的或者是按顺序。当一轮更新结束后，更新步长的最大值少于预设阈值时，终止迭代。
最小角回归法
最小角回归法运用到了前向选择法（选取余弦距离最小的值进行投影，计算残差，迭代这个过程，直到残差达到我们的较小值或者已经遍历了整个变量）和前向梯度算法（选取余弦距离最小的值的样本方向进行移动一定距离，计算残差，重复这个迭代过程）的综合，做法就是取投影方向和前向梯度算法的残差方向形成的角的平分线方向，进行移动。对前向梯度算法和前向选择算法做了折中，保留了前向梯度算法一定程度的精确性，同时简化了前向梯度算法一步步迭代的过程。

为什么L2正则化会产生更稠密解？

L2正则化通常被称为权重衰减（weight decay），就是在原始的损失函数后面再加上一个L2正则化项，即全部权重[公式]的平方和，再乘以λ/2n。则损失函数变为：

$$ C = {C_0} + \frac{\lambda }{{2n}}\sum {{w_i}^2} $$

对应的梯度（导数）：

$$ \begin{array}{l} \frac{{\partial C}}{{\partial w}} = \frac{{\partial {C_0}}}{{\partial w}} + \frac{\lambda }{n}w\\ \frac{{\partial C}}{{\partial b}} = \frac{{\partial {C_0}}}{{\partial b}} \end{array} $$

能够发现L2正则化项对偏置 b 的更新没有影响，可是对于权重$w$的更新有影响：
参数的更新步骤如下：

$$ \begin{array}{l} w \to w' = w - \frac{{\eta \lambda }}{n}w - \eta \frac{{\partial {C_0}}}{{\partial w}}\\ \;\;\;\;\;\;\;\;\;\;\;\; = (1 - \frac{{\eta \lambda }}{n})w - \eta \frac{{\partial {C_0}}}{{\partial w}} \end{array} $$

这里的参数都是大于0的，所以 $1 - \frac{{\eta \lambda }}{n}<1$,因此在梯度下降过程中，权重$w$将逐渐减小，趋向于0但不等于0。这也就是权重衰减（weight decay）的由来。< p>

L2正则化起到使得权重参数$w$变小的效果，为什么能防止过拟合呢？因为更小的权重参数$w$意味着模型的复杂度更低，对训练数据的拟合刚刚好，不会过分拟合训练数据，从而提高模型的泛化能力。

L1和L2的区别和联系？

相同的点：
都可以用来解决过拟合问题的，提高模型的泛化能力。

不同的点：
l1-norm使用的是每个权重值的绝对值之和，l2-norm使用的是每个权重值的平方和；
l1-norm会得到稀疏解，可用于特征选择，l2-norm不会；
l1-norm下降速度更快。

为什么权重变小可以防止过拟合呢？

还是借助上面的公式来说明下问题：

直观上：算法会在训练过程中梯度下降迭代时损失函数尽量的小，而这需要更多复杂的参数，就容易导致过拟合，加上L2之后，当参数变多变复杂时就会导致L2正则化项增大，从而导致损失函数增大，达到制约参数的目的。

模型复杂度：更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合更好(这个法则也叫做奥卡姆剃刀)，而在实际应用中，也验证了这一点，L2正则化的效果往往好于未经正则化的效果。

数学方面：过拟合的时候，拟合函数a的系数往往非常大，为什么?如下图所示，过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着数据在某些小区间内的导数值(绝对值)非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。而正则化是通过约束参数的大小，使其不要太大，所以可以在一定程度上减少过拟合情况。

为什么增加样本可以减少过拟合？

增加的数据主要会引入学习器没有看到过的样本，其中可能包括测试集的分布，这样让模型开开眼界，不会局限于当前数据的分布。
但是如果引入的数据和未来的样本完全不相似，例如不均衡学习中的许多上采样的方法，纯粹基于训练数据的一些加减计算，难以扩充和未来相似的样本，自然是不能缓解过拟合问题了。

参考

https://zhuanlan.zhihu.com/p/72038532
https://zhuanlan.zhihu.com/p/64127398
https://zhuanlan.zhihu.com/p/495738409

检验方法

比较检验方法有哪些？

假设检验——二项检验
假设检验——t检验
交叉验证t检验
McNemar检验
Friedman检验和Nemenyi后续检验

什么是假设检验？

假设检验是用来判断样本与样本，样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。其基本原理是先对总体的特征作出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。

举两个例子：1.在产品的质量检验中经常会遇到的问题就是样本是否可以代替总体，这就涉及用样本来估计总体。2.你先后做了两批实验，得到两组数据，你想知道在这两试实验中合格率有无显著变化，那怎么做呢？这时你可以使用假设检验这种统计方法，来比较你的数据。可以先假设这两批实验合格率没有显著变化，然后用统计的方法推断假设成立的概率，如果是小概率事件，那么原假设不成立。

简述假设检验的一般步骤？

建立原假设和备择假设。
在原假设成立的前提下，选择合适统计量的抽样分布，计算统计量的值，常用的有Z 分布、T 分布、F 分布。
选定显著性水平，查相应分布表确定临界值，从而确定原假设的拒绝区间和接受区间。
对原假设做出判断和解释，如果统计量值大于临界值，拒绝原假设。反之，则接受

什么是置信区间？

任何测量的数据都会存在误差，即使实验条件再精确也无法完全避免随机干扰的影响，所以科学实验往往要测量或实验多次，用取平均值之类的手段去取得结果。多次测量是个排除偶然因素的好办法，但再好的统计手段也不能把所有的偶然因素全部排除。所以，在科学实验中总是会在测量结果上加一个误差范围，这里的误差范围（区间）在统计概率中就叫做置信区间。

为什么小样本用t检验？

从抽样研究所得的样本均数特点来看，只要样本量>60，（无论总体是否服从正态分布）抽样研究的样本均数服从或者近似服从正态分布；而如果样本量较小（参考样本量<100）,抽样分布随着样本量的减小，与正态分布的差别越来越大。此时需要用小样本理论来解释样本均数的分布——而t分布就是小样本理论的代表。因此，小样本的检验需要用到t检验。

各中检验方法的适用范围是什么？

T检验又叫做student t检验，即Student’s t test，通常用于样本含量较小(一般n<30)，总体标准差σ未知的正态分布。目的为：比较样本均数所代表的未知总体均数μ和已知总体均数μ0.

Z检验是通常用于大样本(也就是样本容量>30)平均值差异性检验的方法。是用标准正态分布的理论来推断差异发生的概率，从而对两个平均数的差异进行比较，判断该差异是否显著。

卡方检验又叫做X2检验，简单来说就是，检验两个变量之间有没有关系。卡方检验属于非参数检验，通常是用来比较两个及两个以上样本率(构成比)，以及两个分类变量的关联性分析。基本思想为：比较理论频数和实际频数的吻合程度或者拟合优度问题。

F 检验是为检验方差是否有显著性差异。经常被叫做，联合假设检验(joint hypotheses test)，也可以叫做方差比率检验、方差齐性检验。F 检验为一种在零假设(null hypothesis, H0)情况之下，统计值服从F-分布的检验。

参考

https://zhuanlan.zhihu.com/p/409625718
机器学习-西瓜书
https://zhuanlan.zhihu.com/p/93182578
https://blog.csdn.net/weixin_39875181/article/details/78612348
https://blog.csdn.net/m0_37228052/article/details/121498111
https://blog.csdn.net/qq_48988106/article/details/121113200

模型评估

什么是模型的泛化能力？

泛化能力：指模型对未知的、新鲜的数据的预测能力，通常是根据测试误差来衡量模型的泛化能力，测试误差越小，模型能力越强；
统计理论表明：如果训练集和测试集中的样本都是独立同分布产生的，则有模型的训练误差的期望等于模型的测试误差的期望。

模型评估的方法主要有哪些？

留出法
交叉验证
自助法

Bootstrap原理以及抽样到的概率是啥？

63.2%原始数据元组将出现在自助样本中，而其他36.8%的元组将形成检验集。假设每个元组被选中的概率是 1/d, 因此未被选中的概率是（1-1/d）, 需要挑选 d 次，因此一个元组在 d 次都未被选中的概率是（1-1/d）^d。如果 d 很大，该概率近似为 e^(-1)=0.368。因此36.8%的元组将作为验证集。

自助法优缺点？

自助法的优点有：
在数据集比较小、难以有效划分训练/测试集时很有用：
能从初始数据集中产生多个不同的训练集，这对集成学习等方法而言有很大好处。

但也存在如下缺点：
产生的数据集改变了初始数据集的分布，这会引入估计偏差。因此在初始数据量足够时，留出法和折交叉验证法更常用。

交叉验证的方法主要分为哪些？

1.Holdout验证
严格意义上来说的话，这个不算是交叉验证，因为根本没有用到交叉。首先，我们随机的将样本数据分为两部分（比如：70%的训练集，30%的测试集），然后用训练集来训练模型，在测试集上验证模型及参数。
2.K折交叉验
也是经常会用到的一种方法。主要思想是将数据集划分为互斥的K个集合，用K-1个集合做训练，然后剩下的一个做验证，这里不做过多的解释。
3.留一交叉验证
假设有N个训练样本，它的思想是每次选择N-1个样本来训练数据，留一个样本来验证模型预测的好坏。此方法主要用于样本量非常少的情况，比如对于普通适中问题，当样本小于50时，我一般采用留一交叉验证。

k折交叉验证中k取值多少有什么关系？

在理想情况下，可认为K折交叉验证可以降低模型的方差，从而提高模型的泛化能力，通俗地说，我们期望模型在训练集的多个子数据集上表现良好，要胜过单单在整个训练数据集上表现良好。（但实际上，由于我们所得到K折数据之间并非独立而存在相关性，K折交叉验证到底能降低多少方差还不确定，同时带来的偏差上升有多少也还存疑。）

完全不使用交叉验证是一种极端情况，即K=1的情况下。在这个情况下所有数据都被用于训练，因而过拟合导致低偏差、高方差(low bias and high variance)。留一法是K折的另一种极端情况，即K=n。随着K值的不断升高，单一模型评估时的方差逐渐加大而偏差减小。但从总体模型角度来看，反而是偏差升高了而方差降低了。所以当K值在1到n之间的游走，可以理解为一种方差和偏差妥协的结果。
2017年的一项研究给出了另一种经验式的选择方法，作者建议k=log(n) 且保证n/K>3d ，n代表了数据量，d代表了特征数。
1、使用交叉验证的根本原因是数据集太小，而较小的K值会导致可用于建模的数据量太小，所以小数据集的交叉验证结果需要格外注意。建议选择较大的K值。
2、当模型稳定性较低时，增大K的取值可以给出更好的结果
3、相对而言，较大的K值的交叉验证结果倾向于更好。但同时也要考虑较大K值的计算开销。

训练集、验证集合测试集的作用？

训练集：主要就是训练模型，理论上越大越好；
验证集：用于模型调试超参数。通常要求验证集比较大，避免模型会对验证集过拟合；
测试集：用于评估模型的泛化能力。理论上，测试集越大，评估结果就约精准。另外，测试集必须不包含训练样本，否则会影响对模型泛化能力的评估。
验证集和测试集的对比：

测试集通常用于对模型的预测能力进行评估，它是提供模型预测能力的无偏估计；如果不需要对模型预测能力的无偏估计，可以不需要测试集；
验证集主要是用于超参数的选择。

划分数据集的比例选择方法?

对于小批量数据，数据的拆分的常见比例为：
如果未设置验证集，则将数据三七分：70% 的数据用作训练集、30% 的数据用作测试集。
如果设置验证集，则将数据划分为：60% 的数据用作训练集、20%的数据用过验证集、20% 的数据用作测试集。
对于大批量数据，验证集和测试集占总数据的比例会更小。
对于百万级别的数据，其中 1 万条作为验证集、1 万条作为测试集即可。
验证集的目的就是验证不同的超参数；测试集的目的就是比较不同的模型。
一方面它们要足够大，才足够评估超参数、模型。
另一方面，如果它们太大，则会浪费数据（验证集和训练集的数据无法用于训练）

调参的方法有哪些？

传统的手工调参
在传统的调参过程中，我们通过训练算法手动检查随机超参数集，并选择符合我们目标的最佳参数集。没办法确保得到最佳的参数组合。这是一个不断试错的过程，所以，非常的耗时。
网格搜索
网格搜索是一种基本的超参数调优技术。它类似于手动调优，为网格中指定的所有给定超参数值的每个排列构建模型，评估并选择最佳模型。由于它尝试了超参数的每一个组合，并根据交叉验证得分选择了最佳组合，这使得GridsearchCV非常慢。
随机搜索
使用随机搜索代替网格搜索的动机是，在许多情况下，所有的超参数可能不是同等重要的。随机搜索从超参数空间中随机选择参数组合，参数由n_iter给定的固定迭代次数的情况下选择。实验证明，随机搜索的结果优于网格搜索。随机搜索的问题是它不能保证给出最好的参数组合。
贝叶斯搜索
贝叶斯优化属于一类优化算法，称为基于序列模型的优化(SMBO)算法。这些算法使用先前对损失 f 的观察结果，以确定下一个(最优)点来抽样 f。要在2维或3维的搜索空间中得到一个好的代理曲面需要十几个样本，增加搜索空间的维数需要更多的样本。

在确定参数的最佳组合的保证和计算时间之间总是存在权衡。如果超参数空间(超参数个数)非常大，则使用随机搜索找到超参数的潜在组合，然后在该局部使用网格搜索(超参数的潜在组合)选择最优特征。

参考

https://blog.51cto.com/u_8985428/3866903

性能度量

TP、FP、TN、FN具体指的是什么？

FN：False Negative,被判定为负样本，但事实上是正样本。
FP：False Positive,被判定为正样本，但事实上是负样本。
TN：True Negative,被判定为负样本，事实上也是负样本。
TP：True Positive,被判定为正样本，事实上也是证样本。

ROC曲线和PR曲线的区别？

ROC曲线的纵坐标是TPR，横坐标是FPR
PR曲线的纵坐标是Precision，纵坐标是Recall

其中TPR、FPR以及Precision、Recall的计算方法如下：

$$ \begin{array}{l} TPR = \frac{{TP}}{{TP + FN}}\\ FPR = \frac{{FP}}{{FP + TN}}\\ \Pr ecision = \frac{{TP}}{{TP + FP}}\\ {\mathop{\rm Re}\nolimits} call = \frac{{TP}}{{TP + FN}} \end{array} $$

注意看到TPR就是Recall。

如何综合precision和recall指标？

可以使用 F1评分（F1-Score）：查全率和查准率的调和平均数。

$$ F1 = \frac{{2PR}}{{P + R}} $$

所谓调和平均数，考虑的是，赋予较小值更大的权重，避免较小值和较大值对结果产生较大影响。对于二分类的情况，则讲究的是不偏科。因为我们追求的就是更高的查全率和更高的查准率，即刚才思考中的情况4。因此F1评分相较于单一的查全率和查准率具备更好的评估效果。

Precision和Recall的应用场景？

Precision适用于那些对预测结果很有信心的场景下，比如买股票，希望只要自己选择的标签为1股票，都是涨的；或者在推荐中给用户推荐的视频或者新闻等内容，用户肯定会消费的。

Recall适用于对标签也就是实际上的正样本有很大注意的场景，比如抓坏人，总是希望将坏人都抓回来，因此多抓了几个好人也没事，只要能把坏人抓回来就可以，而不关系自己抓的人中有多少被误伤的。

如何判断一个学习器的性能比另一个好？

如果一个学习器的P-R曲线被另一个学习器的P-R曲线完全包住，则可认为后者的性能优于前者，例如上面的A和B优于学习器C。

ROC曲线中，高于和低于对角线表示意义?

如果模型的roc曲线在对角线下方，则该模型比随机模型还差，高于对角线则表示模型比随机模型好，模型是有意义的。

ROC曲线下的面积就AUC，其中AUC大于0.5表示模型的排序能力是正向的，最起码比随机要好，如果小于0.5，说明模型的排序结果很差了。

多分类AUC怎么算？

基于macro的策略：ovr的划分方式，分别计算每个类别的metrics然后再进行平均

基于micro的策略：所有类放在一起算metrics；

micro的评估方式，当类别非常不均衡时，micro的计算结果会被样本数量多的类别主导，此时需要使用macro

ROC曲线和PR曲线的区别，适用场景，各自优缺点？

roc曲线和正负样本的比例是没有关系的，roc聚焦于二分类模型整体对正负样本的预测能力，所以适用于评估模型整体的性能，如在rank算法中，如果主要关注正样本的预测能力而不care负样本的预测能力，则pr曲线更合适。

准确率Accuracy的局限性是什么？

说明下Accuracy的计算公式如下所示：

$$ A = \frac{{TP + FP}}{{TP + FN + TN + FP}} $$

准确率是分类问题最简单也是最直接的评价标准，但存在明显的缺陷。如：当负样本数占99%时，分类器把所有样本都预测为负样本也可以获得99%的准确率。所以，当不同类别的样本比例非常不均衡时，占比大的类别往往成为影响准确率的最主要因素。

AUC的物理意义是啥?

AUC是衡量排序能力的好坏，越大越好，值在0和1之间，AUC 的原始定义是 ROC 下的面积，计算起来比较麻烦。从ROC 的曲线可以看出， AUC的值不会超过1。同时，对于相同的 FPR ，当 TPR 越大时，面积越大，即 AUC 越大。这也就是说，被模型预测为正的样本中，实际的正样本越多越好，实际的负样本越少越好。从另外一个角度来说， AUC的物理意义就是：随机选出一对正负样本，模型对正样本的打分大于对负样本打分的概率。

$$ AUC = \frac{{\sum {{r_i} - \frac{{P*(P + 1)}}{2}} }}{{P*N}} $$

其中P表示正样本数量，N表示负样本数量, 以及r表示排序值。

AUC为啥对正负样本比例不敏感？

AUC的全称是 area under the curve，即曲线下的面积，通常这里的曲线指的是受试者操作曲线(Receiver operating characteristic, ROC)。实际的模型的ROC曲线则是一条上凸的曲线，介于随机和理想的ROC曲线之间。而ROC曲线下的面积，即为AUC的表达式：

$$ % MathType!MTEF!2!1!+- AUC{\rm{ = }}\int_{t = - \infty }^\infty {y(t)dx(t)} $$

可以证明得到如下的结果：AUC可以看做随机从正负样本中选取一对正负样本，其中正样本的得分大于负样本的概率，证明如下：

为啥很多工程上的评价指标使用ROC或AUC

ROC和AUC是用来衡量模型的排序能力的，可能预测的precision和recall很差，但是AUC很好，在一些推荐排序的算法中，经常使用到AUC指标，说白了，就是AUC指关注排序的好坏，不关注精度啥的指标。

PR和ROC的区别？

PR
P-R曲线就是精确率precision vs 召回率recall 曲线，以recall作为横坐标轴，precision作为纵坐标轴。当我们对样本预测后得到概率，通过置信度就可以对所有样本进行排序，再逐个样本的选择阈值，在该样本之前的都属于正例，该样本之后的都属于负例。得到的PR曲线大概长下面这个样子。P-R曲线肯定会经过（0,0）点，比如讲所有的样本全部判为负例，则TP=0，那么P=R=0，因此会经过（0,0）点，但随着阈值点左移，precision初始很接近1，recall很接近0，因此有可能从（0,0）上升的线和坐标重合，不易区分。如果最前面几个点都是负例，那么曲线会从（0,0）点开始逐渐上升，但曲线最终不会到（1,0）点。

ROC
ROC的全称是Receiver Operating Characteristic Curve，中文名字叫“受试者工作特征曲线”，顾名思义，其主要的分析方法就是画这条特征曲线。该曲线的横坐标为假阳性率（False Positive Rate, FPR）,纵坐标为真阳性率（True Positive Rate, TPR）。

根据上述的定义，ROC最直观的应用就是能反映模型在选取不同阈值的时候其敏感性（sensitivity, FPR）和其精确性（specificity, TPR）的趋势走向。不过，相比于上面说的P-R曲线（精确度和召回率），ROC曲线有一个巨大的优势就是，当正负样本的分布发生变化时，其形状能够基本保持不变，而P-R曲线的形状一般会发生剧烈的变化，因此该评估指标能降低不同测试集带来的干扰，更加客观的衡量模型本身的性能。

为啥方差的计算公式分母为n-1?

首先我们解释下自由度的定义，自由度在英文中是这么解释的，In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.通俗的来说就是，n个样本，如果在某种条件下，样本均值是先定的固定的，那么只剩个n-1样本的值是可以变化的，那么自由度就是n-1。

假设现在有3个样本，分别是${X_1}{X_2}{X_3}$。因为样本具有随机性，所以它们取值不定。但是假设出于某种原因，我们需要让样本均值固定，比如说是$\hat X$，此时"有随机性"的样本只有2个。一旦均值固定了，只要知道其中的两个，剩下的一个肯定可以自动求出来。剩下的那个被求出来的就可以理解为被剥夺了一个自由度。所以就这个例子而言，3个样本最终"自由"的只有其中的 2 个。

实上，计算样本方差时，样本均值就需要给定。计算样本均值也就是维基百科里提到的 ‘intermediate step’。如果你去观察计算样本方差的一系列表达式，比如往往最常会被介绍的方差的无偏估计（样本方差）$\frac{1}{{n - 1}}\sum\nolimits_{i = 1}^n {{{({X_i} - \hat X)}^2}}$.其实发现样本均值这一项都包含在内。考虑到方差是衡量数据偏差程度的统计量，计算一下样本均值作为中间步骤的中间量，也不失其合理性。于是，为计算样本方差，样本里原有的n个自由度，有一个自由度被分配给计算样本均值，剩下自由度即为n-1。

为什么使用标准差？

方差是衡量随机变量或一组数据时离散程度的度量。方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是各个样本数据和平均数之差的平方和的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。方差公式的计算公式如下：

$$ S^2_{N}=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\bar{x})^{2} $$

标准差又称均方差，是方差的算数平方根，标准差的公式如下：

$$ S_{N}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\bar{x})^{2}} $$

样本标准差的计算公式为：

$$ S_{N}=\sqrt{\frac{1}{N-1}\sum_{i=1}^{N}(x_{i}-\bar{x})^{2}} $$

可以看到标准差的概念是基于方差的，仅仅是求了一个平方根而已。那么为什么要造出标准差这样一个概念呢？简单来说，方差单位和数据的单位不一致，没法使用，虽然能很好的描述数据与均值的偏离程度，但是处理结果是不符合我们的直观思维的。而标准差和数据的单位一致，使用起来方便。内在原因就是方差开了一个平方，而标准差通过加了一个根号使得和均值的量纲（单位）保持了一致，在描述一个波动范围时标准差比方差更方便。

与方差相比，使用标准差来表示数据点的离散程度有3个好处：
1、表示离散程度的数字与样本数据点的数量级一致，更适合对数据样本形成感性认知。
2、表示离散程度的数字单位与样本数据的单位一致，更方便做后续的分析运算。
3、在样本数据大致符合正态分布的情况下，标准差具有方便估算的特性：68%的数据点落在平均值前后1个标准差的范围内、95%的数据点落在平均值前后2个标准差的范围内，而99%的数据点将会落在平均值前后3个标准差的范围内。

回归问题的评价指标有哪些？

回归问题五大评价指标分别为

皮尔逊相关系数
解释方差分数（explained_varience_score）
平均绝对误差（mean_absolute_error）
均方差(mean_square_error)
r2分数（r2_score）
调整r2分数（r2_score_adjust）

皮尔逊相关系数怎么算的？

公式计算如下：

$$ {\rho _{X,Y}} = \frac{{Cov(X,Y)}}{{{\sigma _X}{\sigma _Y}}} $$

主要有以下两个步骤：

计算协方差
计算标准差

参考

https://www.zhihu.com/question/20534502/answer/2028365946
https://www.cnblogs.com/13224ACMer/p/11799030.html
https://zhuanlan.zhihu.com/p/386064764
https://blog.csdn.net/dylan_young/article/details/121222221

数据治理

机器学习中如何处理类别型特征？

类别型特征指的是如性别(男、女)，身高(高、矮)等非连续型的数据，这些数据需要经过处理才可以进入到算法模型中
在机器学习中，一般可以按照如下进行处理：

序号编码
序号编码（Ordinal Encoding）通常用于处理类别间具有大小关系的数据。如成绩有“高、中、低”，并且存在“高>中>低”的关系，可以按照大小关系赋予数值ID：3，2，1。
独热编码
独热编码（One-hot Encoding）通常用于处理类别间不具有大小关系的特征，每个类别对应一维编码，如大和小两个特征值可以变为[0,1]和[1,0]
二进制编码
二进制编码（Binary Encoding）是指使用二进制来表示映射关系的编码方式。
1）先将类别特征赋予一个数值型的唯一ID（十进制的整数）
2）将每个类别特征对应的数值型的唯一ID转换成二进制

机器学习中的异常值如何处理？

异常点的检测按照处理方式可以分为图形法和模型法。图形法主要是借助箱线图或者正态分布图来判断，而模型法主要是建立总体模型，偏离模型的鉴定为异常点。

数据错误
不符合直观的数据，如升高为10m,这种数据需要去除，或者使用均值等方法填充。
箱线图
我们常用的分位点为上四分位数q1（数据的75%分位点所对应的值）、中位数（数据的50%分位点所对应的值）和下四分位数q3（数据的25%分位点所对应的值），上下四分位数差值被称为四分位差，即q1-q3。异常点为上须和下须之外的数据点，其中上须=q1+1.5*(q1-q3)，下须=q3-1.5*(q1-q3)。图中中间部分的两个点分别为中位数和均值，可以反映数据的集中趋势。
正态分布图
在数据服从正态分布的情况下，可以借助3∂原则来对异常值进行检测
模型方法
可以使用一些异常检测的方法来进行检测，如AutoEncoder等

缺失值的处理方法有哪些？

不做任何处理
不对丢失的数据做任何事情。一方面，有一些算法有处理缺失值的能力，此时我们可以将完全控制权交给算法来控制它如何响应数据，如xgboos等。另一方面，各种算法对缺失数据的反应不同。例如，一些算法基于训练损失减少来确定缺失数据的最佳插补值。
不使用时将其删除
排除具有缺失数据的记录是一个最简单的方法。但可能会因此而丢失一些关键数据点。
均值插补
使用这种方法，可以先计算列的非缺失值的均值，然后分别替换每列中的缺失值，并独立于其他列。最大的缺点是它只能用于数值数据。这是一种简单快速的方法，适用于小型数值数据集。但是，存在例如忽略特征相关性的事实的限制等。每次填补仅适用于其中某一独立的列。
此外，如果跳过离群值处理，几乎肯定会替换一个倾斜的平均值，从而降低模型的整体质量。
中位数插补
解决上述方法中的异常值问题的另一种插补技术是利用中值。排序时，它会忽略异常值的影响并更新该列中出现的中间值。
众数插补
这种方法可应用于具有有限值集的分类变量。有些时候，可以使用最常用的值来填补缺失值。
分类值的插补
当分类列有缺失值时，可以使用最常用的类别来填补空白。如果有很多缺失值，可以创建一个新类别来替换它们。
前一次观测结果
这是一种常见的统计方法，用于分析纵向重复测量数据时，一些后续观察缺失。
线性插值
这是一种近似于缺失值的方法，沿着直线将点按递增顺序连接起来。简而言之，它以与在它之前出现的值相同的升序计算未知值。因为线性插值是默认的方法，我们不需要在使用它的时候指定它。这种方法常用于时间序列数据集。
KNN 插补
一种基本的分类方法是 k 最近邻 (kNN) 算法。类成员是 k-NN 分类的结果。
项目的分类取决于它与训练集中的点的相似程度，该对象将进入其 k 个最近邻中成员最多的类。如果 k = 1，则该项目被简单地分配给该项目最近邻居的类。使用缺失数据找到与观测值最近的 k 邻域，然后根据邻域中的非缺失值对它们进行插补可能有助于生成关于缺失值的预测。

如何进行连续特征离散化？

无监督学习方法：

等宽法
等频法
基于聚类的方法

有监督学习方法：

1R方法
基于信息熵的方法
基于卡方的方法

什么是特征工程？

特征工程，是指用一系列工程化的方式从原始数据中筛选出更好的数据特征，以提升模型的训练效果。业内有一句广为流传的话是：数据和特征决定了机器学习的上限，而模型和算法是在逼近这个上限而已。由此可见，好的数据和特征是模型和算法发挥更大的作用的前提。

特征工程的步骤有哪些？

一般包括三个子模块：特征构建->特征提取->特征选择

特征构建：根据原始数据构建新的特征，需要找出一些具有物理意义的特征。
特征提取：自动地构建新的特征，将原始特征转换为一组具有明显物理意义或者统计意义或核的特征。例如 Gabor、几何特征、纹理等。常用的方法有：PCA、ICA、LDA等。
特征选择：从特征集合中挑选一组最具统计意义的特征子集，把无关的特征删掉，从而达到降维的效果

特征离散化有什么好处？

在工业界，很少直接将连续值作为逻辑回归模型的特征输入，而是将连续特征离散化为一系列0、1特征交给逻辑回归模型，这样做的优势有以下几点：

离散特征的增加和减少都很容易，易于模型的快速迭代；
稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；
离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；
特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。

特征归一化有哪些方法？

线性归一化
也称min-max标准化、离差标准化；是对原始数据的线性变换，使得结果值映射到[0,1]之间。转换函数如下：

$$ x' = \frac{{x - \min (x)}}{{\max (x) - \min (x)}} $$

这种归一化比较适用在数值较集中的情况。但是这种方法有一个缺陷，就是如果max和min不稳定的时候，很容易使得归一化的结果不稳定，易受极值影响，影响后续使用效果。所以在实际应用中，我们一般用经验常量来替代max和min。

标准差归一化
也叫Z-score标准化，这种方法给予原始数据的均值（mean，μ）和标准差（standard deviation，σ）进行数据的标准化。经过处理后的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：

$$ {x^*} = \frac{{x - u}}{\sigma } $$

非线性归一化
这种方法一般使用在数据分析比较大的场景，有些数值很大，有些很小，通过一些数学函数，将原始值进行映射。一般使用的函数包括log、指数、正切等，需要根据数据分布的具体情况来决定非线性函数的曲线。

特征选择有哪些方法？

筛选特征的方法：过滤式(filter)、包裹式(wrapper)、嵌入式(embedding)

过滤式(filter)
先对数据集进行特征选择，其过程与后续学习器无关，即设计一些统计量来过滤特征，并不考虑后续学习器问题。如方差选择、卡方检验、互信息
包裹式(wrapper)
实际上就是一个分类器，如Las Vagas 算法；包裹式特征选择直接把最终将要使用的学习器的性能作为特征子集的评价原则。其目的就是为给定学习器选择最有利于其性能、量身定做的特征子集。
嵌入式(embedding)
实际上是学习器自主选择特征。如基于惩罚项的选择、基于树的选择GBDT；嵌入式特征选择是将特征选择与学习器训练过程融为一体，两者在同一个优化过程中完成的。即学习器训练过程中自动进行了特征选择。

特征筛选如何获取高相似性特征？

在得到特征后，可以基于卡方或者皮尔逊等相关系数

计算特征之间的相关性方法有哪些？

pearson系数PLCC
对定距连续变量的数据进行计算。是介于-1和1之间的值
Spearman秩相关系数SRCC
该系数是度量两个变量之间的统计相关性的指标，用来评估当前单调函数来描述俩个变量之间的关系有多相关
Kendall（肯德尔等级）相关系数
该相关系数是一个用来测量两个随机变量相关性的统计值。

如何检查数据中的噪声？

通过寻找数据集中与其他观测值及均值差距最大的点作为异常
聚类方法检测：将类似的取值组织成“群”或“簇”，落在“簇”集合之外的值被视为离群点。

什么是组合特征？

为了提高复杂关系的拟合能力，在特征工程中经常会把一阶离散特征两两组合，构成高级特征。例如，特征a有m个取值，特别b 有n个取值，将二者组合就有m*n个组成情况。这时需要学习的参数个数就是 m×n 个。一些常见的算法如FM就可以用来对高维系数特征的交叉进行学习，且在高维情况下可以高效。

如何处理高维特征？

高维连续特征
这种情况可以使用降维方法将维度降低下来然后进行模型的训练，或者对特征进行选择性的筛选得到重要特征后再进行算法开发。
高维离散特征
目前主流的方法是使用Embedding技术进行获取离散特征对应的稠密特征，然后在上层进行特征的融合。

不平衡问题

如何处理类别不均衡问题？

采样
这里的采样可以分为上采样和下采样，简单说就是从类别少的多采样或者类别多的少采样。对于上采样，如SMOTE算法。
转化为One-class问题
把它看做一分类（One Class Learning）或异常检测（Novelty Detection）问题。这类方法的重点不在于捕捉类间的差别，而是为其中一类进行建模，经典的工作包括One-class SVM等
聚类+采样
对数据先进行聚类，再将大的簇进行随机欠采样或者小的簇进行数据生成，注意了，这里不是简单的上面所说的下采样，而是先聚类后再采样。
模型惩罚
简单说就是对分类器的小类样本数据增加权值，降低大类样本的权值。
换模型
使用一些如Bagging和Boosting的方法,

分类问题中如何解决正负样本比较大的情况？

1.随机欠采样（RandomUnder-Sampling）
2.随机过采样（RandomOver-Sampling）
3.基于聚类的过采样（Cluster-BasedOver Sampling）
在这种情况下，K-均值聚类算法独立地被用于少数和多数类实例。这是为了识别数据集中的聚类。随后，每一个聚类都被过采样以至于相同类的所有聚类有着同样的实例数量，且所有的类有着相同的大小。
4.信息性过采样：合成少数类过采样技术（SMOTE）
这一技术可用来避免过拟合——当直接复制少数类实例并将其添加到主数据集时。从少数类中把一个数据子集作为一个实例取走，接着创建相似的新合成的实例。这些合成的实例接着被添加进原来的数据集。新数据集被用作样本以训练分类模型。
5.改进的合成少数类过采样技术（MSMOTE）
6.算法集成技术（AlgorithmicEnsemble Techniques）如 Bagging boosting

采样后如何计算指标？

比如采样前的正负样本比例是100:1, 采样后是1:1，使用采样后的数据训练好的模型后，不是在1:1的数据上验证指标的好坏，而是要在原始的数据上验证precision和recall等。

如果把不平衡的训练集采样到平衡，计算的AUC和Precision会右什么变化？

对于正负样本比为1：100，经过采样后训练得到的模型，在采样后的得到平衡的数据上，相比于之前的不平衡的情况，AUC不会变，这是我们在之前说到的，但是Precision会变大，因为正样本的比例变大了。

class_weight的思想是什么？

就是简单的类权重，对于不平衡的问题的话，可以给不同比例的样本在损失函数函数上加以权重，保持后续在梯度更新上，模型的学习不会偏向于多类的样本，这点在sklearn中的很多模型中都自带的有参数设置。

讲讲smote算法的原理?

SMOTE的全称是Synthetic Minority Over-Sampling Technique 即“人工少数类过采样法”，非直接对少数类进行重采样，而是设计算法来人工合成一些新的少数样本。

主要步骤如下：

选一个正样本
找到该正样本的K个近邻（假设K = 3）
随机从K个近邻中选出一个样本
在正样本和随机选出的这个近邻之间的连线上，随机找一点。这个点就是人工合成的新正样本了

smote的缺点以及为啥在业界用的不多？

SMOTE是基于距离的度量，然后生成少数类样本。这样生成的数据很大可能是噪音数据，是不利于学习的。
原因是：

如果小样本数据之间生成新的小样本数据，没有揭示太多信息，意义不大。
如果小样本数据生成的数据散布在大样本数据里，则很有可能是噪音，意义也不大。

而且工业界的数据量都特别大，对于这种方法需要进行合成数据的效率问题来说，是很难接受的。

过采样和生成样本的区别？

上采样不一定是生成具体的样本，例如简单的重复的进行数据的采样，通过这种采样来说它是不涉及样本生成的过程，但生成样本一定是一种上采样的过程。

参考

https://blog.csdn.net/m0_38068876/article/details/122736423
https://zhuanlan.zhihu.com/p/457807729
https://zhuanlan.zhihu.com/p/91125751
https://blog.csdn.net/weixin_46838716/article/details/124424903
https://blog.csdn.net/cc13186851239/article/details/114336039#69__76
https://zhuanlan.zhihu.com/p/36503570