算法工程师的日常
0%

动态规划

发表于 更新于 分类于 ，

总结

大纲

相关细节

  1. 如果题目求最大值，则dp初始化为[-float(“inf”)]*n的数据
  2. 循环比较一般使用dp[i] = max(dp[i], dp[j] + nums[i])，而不是dp[i] = max(dp[i], dp[j]) + nums[i]

序列

单序列

模板

  • 一般初始化的时候，都会dp = [0] * len(str),而不是dp = [0] * (len(str)+1)
  • 注意有的时候不是输出dp[n-1]而是max(dp)
  • 其他点

最长递增子序列[300]

位于 https://leetcode.cn/problems/longest-increasing-subsequence
dp表达式如下

1
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

代码如下

1
2
3
4
5
6
7
8
class Solution(object):
    def lengthOfLIS(self, nums):
        dp = [1] * len(nums)
        for i in range(1, len(nums)):
            for j in range(i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
        return max(dp)

最长连续递增序列[674]

位于 https://leetcode.cn/problems/longest-continuous-increasing-subsequence
dp表达式如下

1
if (nums[i] > nums[i-1]) dp[i] = max(dp[i], dp[i-1] + 1);

代码如下

1
2
3
4
5
6
7
class Solution(object):
    def findLengthOfLCIS(self, nums):
        dp = [1] * len(nums)
        for i in range(1, len(nums)):
            if nums[i] > nums[i-1]:
                dp[i] = max(dp[i], dp[i-1] + 1)
        return max(dp)

最大子数组和[53]

位于 https://leetcode.cn/problems/maximum-subarray

1
2
3
4
5
6
7
class Solution(object):
    def maxSubArray(self, nums):
        dp = [0] * len(nums)
        dp[0] = nums[0]
        for i in range(1, len(nums)):
            dp[i] = max(dp[i-1]+nums[i], nums[i])
        return max(dp)

回文子串[647]

位于 https://leetcode.cn/problems/palindromic-substrings/description/
动规表达式如下

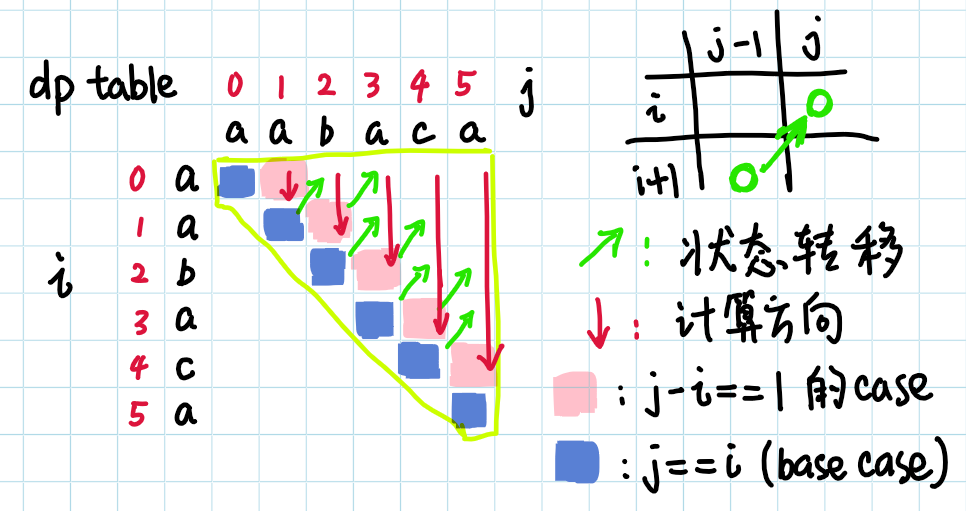
1
2
3
dp[i][i] = 1
if s[i]==s[j] and j-i==1: dp[i][j]=1
if j-i>1 and dp[i+1][j-1] and s[i]==s[j]:dp[i][j]=1

题解如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution(object):
    def countSubstrings(self, s):
        n = len(s)
        dp = [[0]*n for _ in range(n)]
        cnt = 0
        for i in range(n):
            dp[i][i] = 1
            cnt += 1
        for j in range(n):
            for i in range(j):
                if j-i==1 and s[i]==s[j]:
                    dp[i][j] = 1
                    cnt += 1
                elif j -i > 1 and dp[i+1][j-1] and s[i]==s[j]:
                    dp[i][j] = 1
                    cnt += 1
        return cnt

遍历顺序是这样的
image

最长回文子串[5]

位于 https://leetcode.cn/problems/longest-palindromic-substring
子串是连续的，子序列不是，这里要注意，和上面解法一样，代码没变

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution(object):
    def longestPalindrome(self, s):
        n = len(s)
        dp = [[0]*n for _ in range(n)]
        m = 0
        res = None
        for i in range(n):
            dp[i][i] = 1
            if i-i+1>m:
                m = i-i+1
                res = [i,i]
        for j in range(n):
            for i in range(j):
                if j-i==1 and s[i]==s[j]:
                    dp[i][j] = 1
                    if j-i+1>m:
                        m = j-i+1
                        res = [i,j]
                elif j-i>1 and s[i]==s[j] and dp[i+1][j-1]==1:
                    dp[i][j] = 1
                    if j-i+1>m: # 要在里面写不能算完dp后再比较
                        m = j-i+1
                        res = [i,j]
        return s[res[0]:res[1]+1]
# 推荐代码，如果按照上面写法做最长回文子序列会报错，因为循环的时候方向不对的，可以推导一下
class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        dp = [[False] * n for _ in range(n)]
        max_flag = 0
        ind = 0
        for i in range(n):
            dp[i][i] = True
            ind = (i, i)  
        for l in range(1, n):
            for i in range(n - l):
                j = i + l
                if j-i==1 and s[i]==s[j]:
                    dp[i][j] = True
                    if j - i > max_flag: 
                        max_flag = j - i
                        ind = (i, j)
                if j-i>1 and s[i] == s[j]:
                    dp[i][j] = dp[i + 1][j - 1]
                    if dp[i][j] and j - i > max_flag:
                        max_flag = j - i
                        ind = (i, j)
        return (s[ind[0]:ind[1] + 1])

环形子数组的最大和[918]

位于 https://leetcode.cn/problems/maximum-sum-circular-subarray/description/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def maxSubarraySumCircular(self, nums: List[int]) -> int:
        n = len(nums)

        max_ = -float("inf")
        dp_max = [0] * n
        for i in range(n):
            dp_max[i] = max(0, dp_max[i-1]) + nums[i]
            if dp_max[i] > max_:
                max_ = dp_max[i]
        if max(dp_max) < 0:
            return max(nums)
        
        min_ = float("inf")
        dp_min = [0] * n
        for i in range(n):
            dp_min[i] = min(0, dp_min[i-1]) + nums[i]
            if dp_min[i] < min_:
                min_ = dp_min[i]
        
        return max(max_, sum(nums) - min_)

最长回文子序列[516]

位于 https://leetcode.cn/problems/longest-palindromic-subsequence

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        dp = [[0] * len(s) for _ in range(len(s))]
        for i in range(len(s)):
            dp[i][i] = 1
        n = len(s)
        for l in range(1, n):
            for i in range(n - l):
                j = i + l
                if s[i] == s[j]:
                    dp[i][j] = dp[i + 1][j - 1] + 2
                else:
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
        return dp[0][n-1]

戳气球[312]

位于 https://leetcode.cn/problems/burst-balloons

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 递归
class Solution:
    def maxCoins(self, nums: List[int]) -> int:
        n = len(nums)
        val = [1] + nums + [1]
        
        @lru_cache(None)
        def solve(left: int, right: int) -> int:
            if left >= right - 1:
                return 0
            
            best = 0
            for i in range(left + 1, right):
                total = val[left] * val[i] * val[right]
                total += solve(left, i) + solve(i, right)
                best = max(best, total)
            
            return best

        return solve(0, n + 1)
# 动规
class Solution:
    def maxCoins(self, nums: List[int]) -> int:
        n = len(nums)
        rec = [[0] * (n + 2) for _ in range(n + 2)]
        val = [1] + nums + [1]

        for i in range(n - 1, -1, -1):
            for j in range(i + 2, n + 2):
                for k in range(i + 1, j):
                    total = val[i] * val[k] * val[j]
                    total += rec[i][k] + rec[k][j]
                    rec[i][j] = max(rec[i][j], total)
        
        return rec[0][n + 1]

https://leetcode.cn/problems/burst-balloons/solutions/337630/zhe-ge-cai-pu-zi-ji-zai-jia-ye-neng-zuo-guan-jian-/

鸡蛋掉落[887]

位于 https://leetcode.cn/problems/super-egg-drop 本题需要反过来想，如果我们可以做 t 次操作，而且有 k 个鸡蛋，那么我们能找到答案的最高的 n 是多少

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def superEggDrop(self, k: int, n: int) -> int:
        # k鸡蛋，n是楼层
        if n==1:
            return 1
        dp = [[0]*(k+1) for _ in range(n+1)] # t次操作，k个鸡蛋，最高的n
        for i in range(1,k+1):
            dp[1][i] = 1
        ans = -1
        for i in range(2,n+1):
            for j in range(1,k+1):
                dp[i][j] = 1 + dp[i-1][j-1] + dp[i-1][j] # 鸡蛋碎和没碎
            if dp[i][k] >=n: # 注意这里是k
                ans = i
                break
        return ans

建议还是记下来吧，不然很容易忘

双序列

模板

  • 初始化dp为dp=[[0]*(n+1) for _ in range(m+1)],要多一位
  • 在判断的时候要少一位，比如num[i-1]就是对应到dp[i]这里来
  • 初始化一般都是0
  • 注意判断好条件

简单代码如下：

1
2
3
4
5
6
7
8
9
10
n1 = len(text1)
n2 = len(text2)
dp = [[0]*(n2+1) for _ in range(n1+1)] # 注意点1，都为0，且行列为n1+1啊
result = -1
for i in range(1, n1+1): # 注意点2，是从1开始
    for j in range(1, n2+1):
        if text1[i-1] == text2[j-1]: # 注意点3，这里判断i-1是否对的
            dp[i][j] = func(dp[i][j], dp[i-1][j-1] + 1) 
        else:
            dp[i][j] = func(..)

最长重复子数组[718]

位于 https://leetcode.cn/problems/maximum-length-of-repeated-subarray
注意题目中说的子数组，其实就是连续子序列。和最长连续递增序列[674]有点类似，下面的最长公共子序列和最长递增子序列[300]有点像。

dp表达式如下

1
A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;;

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
class Solution(object):
    def findLength(self, nums1, nums2):
        n1 = len(nums1)
        n2 = len(nums2)
        dp = [[0]*(n2+1) for _ in range(n1+1)] # 注意1：这里多了一位
        max_res = -1
        for i in range(1, n1+1):
            for j in range(1, n2+1):
                if nums1[i-1] == nums2[j-1]: # 这里判断i-1,就是       对应dp的i,主要是为了判断方便
                    dp[i][j] = max(dp[i][j], dp[i-1][j-1] + 1)
                max_res = max(max_res, dp[i][j])
        return max_res

最长公共子序列[1143]

位于 https://leetcode.cn/problems/longest-common-subsequence
和 最长重复子数组[718] 不一样，这道题不需要连续的数组。

p表达式如下

1
2
A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;
不等的时候dp[i][j] = max(dp[i-1][j], dp[i][j-1])

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        n1 = len(text1)
        n2 = len(text2)
        dp = [[0]*(n2+1) for _ in range(n1+1)]
        result = -1
        for i in range(1, n1+1):
            for j in range(1, n2+1):
                if text1[i-1] == text2[j-1]:
                    dp[i][j] = max(dp[i][j], dp[i-1][j-1] + 1) 
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
                result = max(result, dp[i][j])
        return result

不相交的线[1035]

位于 https://leetcode.cn/problems/uncrossed-lines
和最长公共子序列一样，代码也是一样的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def maxUncrossedLines(self, nums1, nums2):
        n1 = len(nums1)
        n2 = len(nums2)
        dp = [[0]*(n2+1) for _ in range(n1+1)]
        result = -1
        for i in range(1, n1+1):
            for j in range(1, n2+1):
                if nums1[i-1] == nums2[j-1]:
                    dp[i][j] = max(dp[i][j], dp[i-1][j-1] + 1) 
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
                result = max(result, dp[i][j])
        return result

判断子序列[392]

位于 https://leetcode.cn/problems/is-subsequence
dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 编辑距离的基础题衍生的
class Solution(object):
    def isSubsequence(self, s, t):
        n1 = len(s)
        n2 = len(t)
        dp = [[0]*(n2+1) for _ in range(n1+1)]
        for i in range(1, n1+1):
            for j in range(1, n2+1):
                if s[i-1]==t[j-1]:
                    dp[i][j] = max(dp[i][j],dp[i-1][j-1] + 1)
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        if dp[-1][-1]==len(s):
            return True
        return False

编辑距离[72]

位于 https://leetcode.cn/problems/edit-distance

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        n1 = len(word1)
        n2 = len(word2)
        dp = [[0]*(n2+1) for _ in range(n1+1)]
        for i in range(n1+1):
            dp[i][0] = i
        for j in range(n2+1):
            dp[0][j] = j
        for i in range(1,n1+1):
            for j in range(1, n2+1):
                if word1[i-1]==word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1]) + 1
        return dp[n1][n2]

不同的子序列[115]

位于 https://leetcode.cn/problems/distinct-subsequences
困难题动态规划方程不易想到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        n1 = len(s)
        n2 = len(t)
        dp = [[0]*(n2+1) for _ in range(n1+1)]
        for i in range(n1+1):
            dp[i][0] = 1
        for j in range(n2+1):
            dp[0][j] = 0
        dp[0][0] = 1
        for i in range(1, n1+1):
            for j in range(1, n2+1):
                if s[i-1]==t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j]
        return dp[-1][-1]

两个字符串的删除操作[583]

位于 https://leetcode.cn/problems/delete-operation-for-two-strings

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]
        for i in range(len(word1)+1):
            dp[i][0] = i
        for j in range(len(word2)+1):
            dp[0][j] = j
        for i in range(1, len(word1)+1):
            for j in range(1, len(word2)+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j-1] + 2, dp[i-1][j] + 1, dp[i][j-1] + 1)
        return dp[-1][-1]

爬楼梯类

斐波那契数[509]

位于 https://leetcode.cn/problems/fibonacci-number

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def fib(self, n: int) -> int:
        if n==0:
            return 0
        if n==1:
            return 1
        dp = [0]*(n+1)
        dp[0] = 0
        dp[1]= 1
        for i in range(2, n+1):
            dp[i] = dp[i-1] + dp[i-2]
        return dp[n]

爬楼梯[70]

位于 https://leetcode.cn/problems/climbing-stairs

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def climbStairs(self, n: int) -> int:
        if n==1:
            return 1
        if n==2:
            return 2
        dp = [0] * (n+1)
        dp[0] = 1
        dp[1] = 2
        for i in range(2,n+1):
            dp[i] = dp[i-2] + dp[i-1]
        return dp[n-1]

爬楼梯2[三步问题]

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def waysToStep(self, n: int) -> int:
        run_maps = {1:1,2:2,3:4}
        if n in run_maps:
            return run_maps[n]
        dp = [0] * (n+1)
        dp[1] = 1
        dp[2] = 2
        dp[3] = 4
        for i in range(4, n+1):
            dp[i] = (dp[i-1] + dp[i-2] + dp[i-3])%1000000007
        return dp[n]

爬楼梯3使用最小花费爬楼梯[LCR 088]

位于 https://leetcode.cn/problems/min-cost-climbing-stairs

1
2
3
4
5
6
7
8
class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        dp = [0] * len(cost)
        dp[0] = cost[0]
        dp[1] = cost[1]
        for i in range(2, len(cost)):
            dp[i] = min(dp[i-1], dp[i-2]) + cost[i]
        return min(dp[len(cost)-1],dp[len(cost)-2])

完全平方数[279]

位于 https://leetcode.cn/problems/perfect-squares

1
2
3
4
5
6
7
8
class Solution:
    def numSquares(self, n: int) -> int:
        dp = [float("inf")] * (n+1)
        dp[0] = 0 # 注意
        for i in range(1,n+1):
            for j in range(int(i**0.5)+1):
                dp[i] = min(dp[i], dp[i-j*j]+1)
        return dp[-1]

跳跃游戏[55]

位于 https://leetcode.cn/problems/jump-game

1
2
3
4
5
6
7
8
9
10
class Solution:
    def canJump(self, nums: List[int]) -> bool:
        dp = [0] * len(nums)
        dp[0] = 1
        for i in range(1, len(nums)):
            for j in range(i-1,-1,-1):
                if dp[j] and nums[j] + j >= i:
                    dp[i] = 1
                    break
        return True if dp[len(nums)-1] else False

跳跃游戏II[45]

位于 https://leetcode.cn/problems/jump-game-ii

1
2
3
4
5
6
7
8
9
class Solution:
    def jump(self, nums: List[int]) -> int:
        dp = [float("inf")] * len(nums)
        dp[0] = 0
        for i in range(1, len(nums)):
            for j in range(i):
                if nums[j] + j >= i:
                    dp[i] = min(dp[i], dp[j] + 1)
        return dp[-1]

跳跃游戏 III[1306]

位于 https://leetcode.cn/problems/jump-game-iii
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# BFS
class Solution:
    def canReach(self, arr: List[int], start: int) -> bool:
        from collections import deque
        used = {}
        queue = deque([start])
        while queue:
            node = queue.popleft()
            if arr[node]==0: # 容易写到2出
                return True
            if node in used:
                continue
            used[node] = 1
            for v in [node-arr[node], node+arr[node]]:
                if v >= 0 and v<len(arr):
                    if v in used:
                        continue # 2
                    queue.append(v)
        return False
# DFS
class Solution:
    def canReach(self, arr: List[int], start: int) -> bool:
        s = {}
        def dfs(arr, st):
            if st not in s and arr[st]==0:
                return True
            s[st] = 1
            current_step = arr[st]
            for step in [st+current_step, st-current_step]:
                if step>=0 and step< len(arr) and step not in s and dfs(arr, step):
                    return True
            return False
        return dfs(arr, start)

跳跃游戏 VI[1696]

位于 https://leetcode.cn/problems/jump-game-vi

1
2
3
4
5
6
7
8
9
class Solution:
    def maxResult(self, nums: List[int], k: int) -> int:
        dp = [-float("inf")] * len(nums) # 容易写错
        dp[0] = nums[0]
        for i in range(1, len(nums)):
            for j in range(max(0, i - k), i):
                dp[i] = max(dp[i], dp[j] + nums[i]) 
                # 这里错写为max(dp[i], dp[j] + nums[i])
        return dp[-1]

青蛙过河[403]

位于 https://leetcode.cn/problems/frog-jump

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 递归
class Solution:
    def canCross(self, stones: List[int]) -> bool:
        for i in range(1, len(stones)):
            if stones[i] > i + stones[i-1]:
                return False
        end = stones[-1]
        stones = set(stones)

        @functools.lru_cache(None)
        def dfs(location, step):
            if location == end: return True
            for step in [step-1, step, step+1]:
                if step > 0 and location+step in stones and dfs(location+step, step):
                    return True
            return False
        return dfs(0, 0)
# DP
class Solution:
    def canCross(self, stones: List[int]) -> bool:
        n = len(stones)
        dp = [[False]* n for _ in range(n)]
        dp[0][0] = True
        for i in range(1,n):
            for j in range(i-1,-1,-1):
                k = stones[i] - stones[j]
                if k>j+1:
                    break
                dp[i][k] = dp[j][k] or dp[j][k-1] or dp[j][k+1]
        for i in dp[n-1]:
            if i:
                return True
        return False

不懂看这里 https://www.ai2news.com/blog/2980406/

打家劫舍[198]

位于 https://leetcode.cn/problems/house-robber

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def rob(self, nums: List[int]) -> int:
        if len(nums)==1:
            return nums[0]
        if len(nums)==2:
            return max(nums)
        dp = [0] * len(nums)
        dp[0] = nums[0]
        dp[1] = nums[1]
        for i in range(2,len(nums)):
            for j in range(i-1):
                dp[i] = max(dp[i], dp[j]+nums[i])
                # 容易写错为dp[i] = max(dp[i], dp[j]+nums[j])
        return max(dp)

打家劫舍 II[213]

位于 https://leetcode.cn/problems/house-robber-ii

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def rob(self, nums: List[int]) -> int:        
        def dp_f(nums):
            dp = [0] * len(nums)
            dp[0] = nums[0]
            dp[1] = nums[1]
            for i in range(2,len(nums)):
                for j in range(i-1):
                    dp[i] = max(dp[i], dp[j]+nums[i])
            return max(dp)
        if len(nums)==1:
            return nums[0]
        if len(nums)==2:
            return max(nums)
        max_dp1 = dp_f(nums[0:len(nums)-1])
        max_dp2 = dp_f(nums[1:len(nums)])
        return max(max_dp1, max_dp2)

分开来做就好

打家劫舍 III[337]

位于 https://leetcode.cn/problems/house-robber-iii
递归法，实现思路：用root点和不用root点

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def rob(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        # 用root点
        money = root.val
        if root.left:
            money = money + self.rob(root.left.left) + self.rob(root.left.right)
        if root.right:
            money = money + self.rob(root.right.left) + self.rob(root.right.right)
        return max(money, self.rob(root.left)+self.rob(root.right)) #不用root点

递归优化法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.d = {}

    def rob(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        if root in self.d:
            return self.d[root]
        money = root.val
        if root.left:
            money = money + self.rob(root.left.left) + self.rob(root.left.right)
        if root.right:
            money = money + self.rob(root.right.left) + self.rob(root.right.right)
        result = max(money, self.rob(root.left)+self.rob(root.right))
        self.d[root] = result
        return result

背包零钱

背包问题介绍

可以看如下几个连接，增加对某些点的理解

整体上，背包问题的动态规划写成如下的形式：

0-1背包

1
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w_i]+v_i, 0<=w_i<=j)

完全背包

1
dp[i][j]=max(dp[i-1][j],dp[i][j-w_i]+v_i, 0<=w_i<=j)

注意：在使用的时候，大部分组合问题，因此for两层循环的话，外层是N个物件或者N种币，内层是背包的容量W或者是要凑的零钱大小W。关于组合还有排序的问题可以看 https://leetcode.cn/problems/coin-change-ii/solutions/143948/ling-qian-dui-huan-iihe-pa-lou-ti-wen-ti-dao-di-yo/

逻辑分开

做题的逻辑哈
图片1.png

模板

1
2
3
4
5
6
7
8
9
10
11
12
# 二维
dp[0][0] = x
for i in range(1, n+1):#注意加1
    for j in range(amount+1): #注意加1
        if xx:
            dp[i][j] = min(dp[i-1][j] , dp[i][j-coins[i-1]]+1) # 注意i-1
        else:
            ...
# 一维
for i in coins: # 1. 遍历硬币
    for j in range(amount,i-1, -1): # 2.遍历金额，逆序，注意最小值
        dp[j] = min,max,..., dp[j], dp[j-i] # 3. 写动态函数

0-1背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 二维
N = 3  # 物品数量
W = 4  # 背包容量
Wt = [2, 1, 3]  # 所占用的容量
val = [4, 2, 3]  # 价值
dp = [[0] * (W + 1) for _ in range(N + 1)]
for i in range(1, N + 1):
    for w in range(1, W + 1):
        if w - Wt[i - 1] < 0:
            dp[i][w] = dp[i - 1][w]
        else:
            dp[i][w] = max(dp[i - 1][w], dp[i - 1][w - Wt[i - 1]] + val[i - 1])
# 【推荐写法】一维
def test_1_wei_bag_problem():
    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagWeight = 4

    # 初始化
    dp = [0] * (bagWeight + 1)
    for i in range(len(weight)):  # 遍历物品
        for j in range(bagWeight, weight[i] - 1, -1):  # 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

    print(dp[bagWeight])

目标和[494]

位于 https://leetcode.cn/problems/target-sum

分析：0-1背包，外循环硬币，内循环金额，内循环逆序，注意内循环最小值

dp累加dp[i] = dp[i] + dp[j-i]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# 二维
class Solution(object):
    def findTargetSumWays(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        total = sum(nums)
        if abs(target) > total:
            return 0
        if (total+target)%2==1:
            return 0
        pos = (total + target) // 2
        neg = (total - target) // 2
        C = min(pos,  neg) # 金额
        n = len(nums) # 硬币数量

        dp = [[0]*(C+1) for _ in range(n+1)]
        dp[0][0] = 1
        for i in range(1, n+1):
            for j in range(C+1):
                if j >= nums[i-1]:
                    dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]] # 0-1背包
                else:
                    dp[i][j] = dp[i-1][j]
        return dp[n][C]
        
# 【推荐写法】一维
class Solution(object):
    def findTargetSumWays(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        total = sum(nums)
        if abs(target) > total:
            return 0
        if (total+target)%2==1:
            return 0
        pos = (total + target) // 2
        neg = (total - target) // 2
        C = min(pos,  neg) # 金额
        n = len(nums) # 硬币数量

        dp = [0] * (C+1)
        dp[0] = 1
        for i in nums: # 1. 外循环：遍历硬币 
            for j in range(C, i-1, -1): # 2. 内循环 逆序：遍历目标金额，最小为i-1一定
                dp[j] = dp[j] + dp[j-i]
        return dp[C]

分割等和子集[416]

位于 https://leetcode.cn/problems/partition-equal-subset-sum

分析：0-1背包，外循环硬币，内循环金额，内循环逆序，注意内循环最小值

dp累求|即可，为dp[i] = dp[i] | dp[j-i]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 一维动态规划
class Solution(object):
    def canPartition(self, nums):
        # 边界
        total = sum(nums)
        if total % 2==1:
            return False
        target = total // 2
        if max(nums) > target:
            return False
        # dp
        dp = [False] * (target+1)
        dp[0] = True

        for num in nums: # 1.遍历物品即硬币
            for j in range(target, num-1, -1): # 2. 遍历目标（金额），逆序，最小为num-1
                dp[j] |= dp[j-num] # 3. 动规表达式
        return dp[target]

最后一块石头的重量 II[1049]

位于 https://leetcode.cn/problems/last-stone-weight-ii

分析：0-1背包，外循环硬币，内循环金额，内循环逆序，注意内循环最小值

dp为 dp[j] = max(dp[j], dp[j - stone] + stone)

分析：本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了。分析到物品的重量为stones[i]，物品的价值也为stones[i]。

dp数组含义，表示前i个stone得到不超过taget的最大重量，这里是最大，不是刚刚好。

1
2
3
4
5
6
7
8
9
10
11
12
# 一维动态规划
class Solution:
    def lastStoneWeightII(self, stones: List[int]) -> int:
        dp = [0] * 15001
        total_sum = sum(stones)
        target = total_sum // 2

        for stone in stones:  # 1. 遍历物品
            for j in range(target, stone - 1, -1):  # 2. 遍历背包，逆序，最小为stone-1
                dp[j] = max(dp[j], dp[j - stone] + stone)
                
        return total_sum - dp[target] - dp[target]

一和零[474]

位于 https://leetcode.cn/problems/ones-and-zeroes
分析：0-1背包，外循环硬币，内循环金额，内循环逆序，注意内循环最小值

dp表达式为 dp[m][n] = max(dp[m][n], dp[m-neg][n-pos]+1)

分析：从一个list的字符串中选择一些数，使得1的数不超过m,0的数不超过n.
dp[i][j]表示不超过i和j的最大集合的长度，和上面类似，这是这里二维。

1
2
3
4
5
6
7
8
9
10
class Solution(object):
    def findMaxForm(self, strs, m, n):
        dp = [[0]*(n+1) for _ in range(m+1)]
        for s in strs: # 1. 遍历硬币
            pos = s.count('1')
            neg = len(s) - pos
            for m1 in range(m,neg-1,-1): # 2. 遍历金额，逆序，最小值
                for n1 in range(n,pos-1,-1):# 3. 遍历金额，逆序，最小值
                    dp[m1][n1] = max(dp[m1][n1], dp[m1-neg][n1-pos]+1)
        return dp[m][n]

完全背包

1
2
3
4
5
6
7
8
9
10
11
N = 3  # 物品数量
W = 4  # 背包容量
Wt = [2, 1, 3]  # 所占用的容量
val = [4, 2, 3]  # 价值
dp = [[0] * (W + 1) for _ in range(N + 1)]
for i in range(1, N + 1):
    for w in range(1, W + 1):
        if w - Wt[i - 1] < 0:
            dp[i][w] = dp[i - 1][w]
        else:
            dp[i][w] = max(dp[i - 1][w], dp[i][w - Wt[i - 1]] + val[i - 1])

零钱兑换[322]

位于 https://leetcode.cn/problems/coin-change

分析：完全背包，外循环硬币，内循环金额，内循环顺序

dp公式dp[j] = min(dp[j],dp[j-i]+1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 二维解法
class Solution(object):
    def coinChange(self, coins, amount):
        # 1. 初始化
        N = len(coins)
        dp = [[float("inf")]*(amount+1) for _ in range(N+1)]
        dp[0][0] = 0
        # 2. 循环
        for i in range(1,N+1):
            for j in range(amount+1):
                if j >= coins[i-1]:
                    dp[i][j] = min(dp[i-1][j] , dp[i][j-coins[i-1]]+1)
                else:
                    dp[i][j] = dp[i-1][j]
        ans = dp[N][amount]
        return ans if ans!=float("inf") else -1
# 一维解法I
class Solution(object):
    def coinChange(self, coins, amount):
        # 1. 初始化
        N = len(coins)
        dp = [float("inf")]*(amount+1)
        dp[0] = 0
        # 2. 循环
        for i in range(N):
            for j in range(amount+1):
                if j >= coins[i]:
                    dp[j] = min(dp[j], dp[j-coins[i]]+1)
        return dp[amount] if dp[amount]!=float("inf") else -1
# 一维解法II
class Solution(object):
    def coinChange(self, coins, amount):
        if amount==0:
            return 0
        dp = [float('inf')] * (amount+1)
        dp[0] = 0
        for i in coins:
            for j in range(i, amount+1):
                dp[j] = min(dp[j],dp[j-i]+1)

        return dp[amount] if dp[amount]!=float('inf') else -1

注意一维和二维中，在二维初始化的时候长度是amount+1, 一维也是，但是在N这个地方，二维是N+1，一维是N。

解法 https://leetcode.cn/problems/coin-change/solutions/1412324/by-flix-su7s/

零钱兑换II[518]

位于 https://leetcode.cn/problems/coin-change-ii

分析：完全背包，外循环硬币，内循环金额，内循环顺序

dp公式dp[j] = dp[j] + dp[j-i]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 二维
class Solution(object):
    def change(self, amount, coins):
        # 1. 初始化
        N = len(coins)
        dp = [[0]*(amount+1) for _ in range(N+1)] # 方便后面取数
        dp[0][0] = 1
        # 2. 循环
        for i in range(1, N+1):
            for j in range(amount+1):
                if coins[i-1] > j:
                    dp[i][j] = dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]]
        return dp[N][amount]

当然，官方简单的方法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 1. 压缩为1维
class Solution(object):
    def change(self, amount, coins):
        if not amount:
            return 1      
        # 1. 初始化
        dp = [0] * (amount+1)
        dp[0] = 1
        # 2. 循环
        N = len(coins)
        for i in range(N): 
            for j in range(amount+1):
                if j >= coins[i]:                    
                    dp[j] = dp[j] + dp[j-coins[i]]
        return dp[amount]
# 2.再简化
class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        if not amount:
            return 1      
        dp = [0] * (amount+1)
        dp[0] = 1
        for i in coins: 
            for j in range(i, amount+1):
                dp[j] = dp[j] + dp[j-i]
        return dp[amount]

硬币问题[面试题 08.11]

题目见 https://leetcode-cn.com/problems/coin-lcci 题解如下：

1
2
3
4
5
6
7
8
9
10
class Solution:
    def waysToChange(self, n: int) -> int:
        mod = 10**9 + 7
        coins = [25, 10, 5, 1]

        f = [1] + [0] * n
        for coin in coins:
            for i in range(coin, n + 1):
                f[i] += f[i - coin]
        return f[n] % mod

分割数组的最大值[410]

位于 https://leetcode.cn/problems/split-array-largest-sum
分析：完全背包，外循环硬币，内循环金额，内循环顺序

dp公式f[i][j] = min(f[i][j], max(f[k][j - 1], sub[i] - sub[k]))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    def splitArray(self, nums: List[int], m: int) -> int:
        n = len(nums)
        f = [[10**18] * (m + 1) for _ in range(n + 1)]
        sub = [0]
        for elem in nums:
            sub.append(sub[-1] + elem)
        
        f[0][0] = 0
        for i in range(1, n + 1):
            for j in range(1, min(i, m) + 1):
                for k in range(i):
                    f[i][j] = min(f[i][j], max(f[k][j - 1], sub[i] - sub[k]))
        
        return f[n][m]

组数总和Ⅳ

位于 https://leetcode.cn/problems/combination-sum-iv
分析：完全背包，外循环金额【排列问题】，内循环硬币，内循环顺序

dp公式dp[i] = dp[i] + dp[i-j]

题目见 https://leetcode-cn.com/problems/combination-sum-iv/ 这道题和爬楼梯的问题有点类似，但是解法不太一样。动态规划的方程是
dp[i] = sum(dp[i-j]) j<=i.解法如下

1
2
3
4
5
6
7
8
9
class Solution:
    def combinationSum4(self, nums: List[int], target: int) -> int:
        dp = [0] * (target+1)
        dp[0] = 1
        for i in range(1,target+1):
            for j in nums:
                if i >= j:
                    dp[i] = dp[i] + dp[i-j]
        return dp[-1]

爬楼梯[70]

位于 https://leetcode.cn/problems/climbing-stairs
分析：完全背包，外循环金额【排列问题】，内循环硬币，内循环顺序

dp公式dp[i] = dp[i] + dp[i-j]

1
2
3
4
5
6
7
8
target = 10 # 爬到阶梯数
w = [1, 2, 3] # 每次可以爬多少
dp = [0] * (target + 1)
for i in range(target + 1):
    for j in range(len(w)):
        if i - j >= 0:
            dp[i] = dp[i] + dp[i - j]
print(dp[10])

剪绳子

题目见

股票买卖问题

模板

这里主要说一下DP的思路，按照labuladong的做法，基本上上可以在一个模板上丝毫不动，就可以得到结果

统一的动态规划方程如下

1
2
3
4
5
6
7
8
9
10
11
# 初始化
dp = [[0]*2 for _ in range(len(prics))]
for i in range(len(prices)):
    dp[i][0] = 0
    dp[i][1] = -float("inf")
if i==0:
    dp[i][0] = 0
    dp[i][1] = -prics[0] - 手续费
# for一下
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i] - 手续费)

i表示第几天，k表示最多交易次数，0表示手里没股票了，1表示手里还有股票。

https://labuladong.github.io/algo/di-er-zhan-a01c6/yong-dong--63ceb/yi-ge-fang-3b01b/

买卖股票的最佳时机[121]

题目：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/description/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 模板解法
class Solution(object):
    def maxProfit(self, prices):
        # dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
        # dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]) 
        # k=1简化为
        # dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        # dp[i][1] = max(dp[i-1][1], -prices[i])
        dp = [[0]*2 for i in range(len(prices))]
        for i in range(len(prices)):
            if i == 0:
                dp[i][0] = 0
                dp[i][1] = -prices[0]
                continue
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
            dp[i][1] = max(dp[i-1][1], -prices[i])
        return dp[len(prices)-1][0]
# 更简单做法
class Solution(object):
    def maxProfit(self, prices):
        mins = float("inf")
        profit = 0
        for i in prices:
            if i < mins:
                mins = i
            profit = max(profit, i - mins)
        return profit

买卖股票的最佳时机II[122]

题目：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/description/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 模板做法
class Solution(object):
    def maxProfit(self, prices):
        # dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
        # dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]) 
        # k=1简化为
        # dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        # dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i]) #改动点1
        dp = [[0]*2 for i in range(len(prices))]
        for i in range(len(prices)):
            if i == 0:
                dp[i][0] = 0
                dp[i][1] = -prices[0]
                continue
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])#改动点2
        return dp[len(prices)-1][0]
# 更简单做法
class Solution(object):
    def maxProfit(self, prices):
        profit = 0
        for i in range(1, len(prices)):
            if prices[i] - prices[i-1] > 0:
                profit += prices[i] - prices[i-1]
        return profit

买卖股票的最佳时机含冷冻期[309]

题目：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 模板做法
class Solution(object):
    def maxProfit(self, prices):
        # dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
        # dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]) 
        # k=1简化为
        # dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        # dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
        dp = [[0]*2 for i in range(len(prices))]
        for i in range(len(prices)):
            if i == 0:
                dp[i][0] = 0
                dp[i][1] = -prices[0]
                continue
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-2][0]-prices[i]) # 改动点
        return dp[len(prices)-1][0]

买卖股票的最佳时机含手续费[714]

题目：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/description/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution(object):
    def maxProfit(self, prices, fee):
        # dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
        # dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]) 
        # k=1简化为
        # dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        # dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
        dp = [[0]*2 for i in range(len(prices))]
        for i in range(len(prices)):
            if i == 0:
                dp[i][0] = 0
                dp[i][1] = -prices[0] - fee # 改动点
                continue
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i]-fee) # 改动点
        return dp[len(prices)-1][0]

买卖股票的最佳时机 III[123]

题目：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/description/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        # dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
        # dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]) 
        # k=1简化为
        # dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        # dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
        max_k = 2
        dp = [[[0] * 2 for _ in range(max_k + 1)] for _ in range(len(prices))]
        for i in range(len(prices)):
            for k in range(1, max_k+1): # 改动点
                if i == 0:
                    dp[i][k][0] = 0
                    dp[i][k][1] = -prices[0]
                    continue
                dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
                dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0]-prices[i])
        return dp[len(prices)-1][max_k][0]

博弈问题

https://labuladong.online/algo/dynamic-programming/game-theory/

预测赢家[486]

题目：https://leetcode.cn/problems/predict-the-winner/description/

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def predictTheWinner(self, nums: List[int]) -> bool:
        length = len(nums)
        dp = [[0] * length for _ in range(length)]
        for i, num in enumerate(nums):
            dp[i][i] = num
        for l in range(1,length):
            for i in range(length-l):
                j = i + l
                dp[i][j] = max(nums[i] - dp[i + 1][j], nums[j] - dp[i][j - 1])
        return dp[0][length - 1] >= 0

石子游戏[877]

题目：https://leetcode.cn/problems/stone-game/description/

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def stoneGame(self, piles: List[int]) -> bool:
        length = len(piles)
        dp = [[0] * len(piles) for _ in range(len(piles))]
        for i in range(len(piles)):
            dp[i][i] = piles[i]
        for l in range(1,length):
            for i in range(length-l):
                j = i + l        
                dp[i][j] = max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1])
        return dp[0][length - 1] > 0

和上面一样，严格意义上，不算双序列问题，所以这里不用dp=[[0]*(n+1) for i in range(n+1)]